।। রজত কান্তি দাস।।
 |
| (C)Image:ছবি |
‘Uncle
Petros and Goldbach’s Conjecture’ - উপন্যাস
গণিতের নাম শুনলেই যে সব ছাত্রছাত্রীদের
হৃদকম্পন শুরু হয়ে যায় তাদের জানিয়ে রাখি গণিত বিষয়টি আজ আর এত নিরস হয়ে থাকেনি।
গণিতকে কেন্দ্র করে লেখা হচ্ছে জনপ্রিয় উপন্যাস। বিজ্ঞান, প্রযুক্তি, ব্যাংকিং,
ব্যবসা-বাণিজ্য ইত্যাদি অনেক বিষয়ের উপর
আধিপত্য বিস্তার করে গণিত এখন সাহিত্যের জগতেও ঢুকে পড়েছে। গ্রিক উপন্যাসিক এপোস্তলস দক্সিয়াদিস
গ্রিক ভাষায় এমন এক উপন্যাস লিখেছেন যার মূল বিষয় হচ্ছে গণিতের এক সমাধান না হওয়া বিষয়। উপন্যাসটির
ইংরেজি সংস্করণের
নাম ‘Uncle Petros and Goldbach’s Conjecture’ । উপন্যাসটি সারা পৃথিবীতে এতটাই জনপ্রিয়তা পেয়েছে যে
২৫টির বেশি ভাষায় এর অনুবাদ হয়ে গেছে। যারা এতদিন মনে করতেন গণিতের সঙ্গে সাহিত্যের সম্পর্ক
মেরুসাদৃশ্য তাদের ভুল
ভেঙ্গেছে। আসলে সাহিত্যে অচ্ছুৎ বলে কিছু নেই এবং যারা মনে করেন আছে তারা জানেনই না এর
বিস্তার কতখানি। তাই গণিত নিয়ে উপন্যাস লেখা কোন আশ্চর্যের বিষয় নয়।
১৯৯২ সালে প্রথম প্রকাশিত দক্সিয়াদিসের
এই উপন্যাসটি
পরে ইংরেজিতে অনুদিত হয়ে আমেরিকার ব্লুমস বেরি ও ব্রিটেনের ফ্যাবার এন্ড ফ্যাবার প্রকাশনা সংস্থা
প্রকাশ করে ঘোষণা করেছিল কেউ যদি ‘গোল্ডবাক্স
কনজেকচার’ নামে গণিতের এই
সমাধান না হওয়া সমস্যাটির সমাধান করে দিতে পারেন তাহলে তাকে এক মিলিয়ন মার্কিন ডলার পুরষ্কার দেওয়া
হবে। বলাবাহুল্য
এই পুরষ্কারের কোন দাবিদার বেরোয় নি। কারণ বিগত কয়েক শতাব্দী
ধরে বহু চেষ্টার পরও এই সমস্যাটির
সমাধান হয় নি।
উপন্যাসের কাহিনীর
প্রসঙ্গে আসার আগে আমাদের জানতে হবে এই ‘গোল্ডবাক্স কংজেকচার’ জিনিসটা কি? এটি এমন এক সমস্যা যা জড়িয়ে আছে মৌলিক সংখ্যার উপর। এই
সমস্যাটি যার নামের সঙ্গে
জড়িত তিনি হলেন ক্রিশ্চিয়ান গোল্ডবাক। ১৬৯০ খ্রিস্টাব্দে এই জার্মান গণিতজ্ঞ জন্মেছিলেন
তৎকালীন প্রুশিয়া রাজ্যে। তিনি ঘোষণা করেন ২-এর চাইতে বড় যে কোন জোড় সংখ্যাকে দু’টো মৌলিক সংখ্যার যোগফল দিয়ে প্রকাশ করা
সম্ভব। যেমন
৫০ একটি জোড় সংখ্যা যা ৪৭ ও ৩ দুটি মৌলিক সংখ্যার যোগফল। আবার মনে করুন ৩০ একটি জোড়
সংখ্যা যা ২৩ ও ৭ দুটি মৌলিক সংখ্যার যোগফল। এ রকম সমস্ত জোড় সংখ্যাকেই কোন না কোন দুটি মৌলিক
সংখ্যার যোগফল দিয়ে প্রকাশ করা যায়। আজ পর্যন্ত এমন কোন জোড় সংখ্যা বেরোয় নি যেটিকে দুটো মৌলিক
সংখ্যার যোগফল দিয়ে
প্রকাশ করা যায় না। প্রসঙ্গত বলে রাখি মৌলিক সংখ্যা হলো সেই সংখ্যা যাকে ১ অথবা ঐ সংখ্যা
ছাড়া অন্য যে কোন দুটি বা ততোধিক সংখ্যার গুণফল দিয়ে প্রকাশ করা যায় না। ইদানীং সুপার
কম্পিউটারের সাহায্যে বিশাল অঙ্কের মধ্যবর্তী সমস্ত জোড় সংখ্যাকে পরীক্ষা করে দেখা গেছে যে সত্যিই
এরকম কোন জোড়
সংখ্যা পাওয়া যায় নি যা দুটো মৌলিক সংখ্যার যোগফল নয়। তাহলে সমস্যাটা কোথায়?
সমস্যাটা হলো সংখ্যার যেমন কোন শেষ নেই
তেমনি জোড় সংখ্যারও
শেষ নেই। আবার খ্রিস্টের জন্মের ৩০০ বছর আগেই ইউক্লিড প্রমাণ করেন যে মৌলিক সংখ্যারও
শেষ নেই। তিনি এটি প্রমাণ করেন এইভাবে যে কোন একটি সংখ্যাকে যদি ধরা হয় শেষ মৌলিক সংখ্যা
তাহলে এর আগে যতগুলো মৌলিক সংখ্যা আছে সবগুলোকে গুণ করলে যে সংখ্যাটি পাওয়া যাবে তার সঙ্গে ১ যোগ
করলে ওইটি হবে
এর চাইতে বড় মৌলিক সংখ্যা। অর্থাৎ যেকোনো সংখ্যাকে শেষ মৌলিক সংখ্যা ধরে নিলে দেখা যাবে
এর পরেও মৌলিক সংখ্যা আছে। অতএব স্বাভাবিক সংখ্যার মতো মৌলিক সংখ্যাও অসীম। তাই যেহেতু অসীম
তাই সবগুলো জোড় সংখ্যাকে পরীক্ষা করে দেখা সম্ভব নয়। এর জন্য প্রয়োজন গাণিতিক যুক্তি যা প্রমাণ করবে
যে যেকোনো জোড়
সংখ্যা দুটি মৌলিক সংখ্যার যোগফল হতে বাধ্য। কিন্তু এই গণিতের যুক্তি দিয়ে এটা প্রমাণ
করাটা এমনই কঠিন কাজ যা বিগত কয়েক শতাব্দী ধরে কেউ করতে পারছে না।
উপন্যাসে আঙ্কল পেত্রোস হলেন এক
অসামান্য প্রতিভাবান গণিতজ্ঞ
যার মধ্যে এই আত্মবিশ্বাস জন্মেছিল যে তিনি এই দুরূহ কাজটি সম্পন্ন করতে পারবেন। কিন্তু
এই কাজটি করতে গিয়ে তিনি গণিতের জটিল সমস্যায় এমনই জড়িয়ে পড়েন যে তার উজ্জ্বল ভবিষ্যৎ,
কর্ম জীবন সমস্তই নষ্ট হয়ে যায়। তিনি বিপত্নীক হলেও পরিবার
থেকে বিচ্ছিন্ন হয়ে পড়েন। তার বাবা হতাশাগ্রস্ত হয়ে একদিন বলেই ফেললেন যে তিনি একটি ষাঁড়ের
পেছনে এত অর্থ ব্যয় করে সবচেয়ে ভাল ভাল শিক্ষা প্রতিষ্ঠানে পড়ার সুযোগ করে দিয়েছেন। শেষ জীবনে এই
হতাশ ও হাল ছেড়ে
দেওয়া এক বিশাল সম্ভাবনাময় গণিতজ্ঞের করুণ কাহিনীতে উঠে এসেছে গণিত নিয়ে বহু ধরণের
আলোচনা। উঠে এসেছে ইউরোপের বিভিন্ন বিশ্ববিদ্যালয়ের বেশ কিছু গণিতজ্ঞের নাম যারা বাস্তব জীবনে
আছেন। দক্সিয়াদিস এমন ভাবে এই উপন্যাসের প্লটকে সাজিয়েছেন যা বিশ্বাসযোগ্য বলে মনে হয়।
পেত্রোসের জীবনের পড়ন্ত
বেলায় তিনি যখন একটি ফার্ম হাউসে একাকী জীবনযাপন করতেন তখন তার পরিবারের সদস্যদের
তার সঙ্গে আলাপ করতে নিষেধ করা হয়। কিন্তু এই নিষেধ উপেক্ষা করে তার ভাতিজা এসে কাকাকে
বোঝায় জীবনের শেষ দিন পর্যন্ত পেত্রোস যেন তার চেষ্টা চালিয়ে যান। এভাবে হাল ছেড়ে বসে থাকাটা ঠিক নয়।
সাফল্য যেকোনো
সময় আসতে পারে।
এই উপন্যাসের বেশি বর্ণনা দেওয়া আমার উদ্দেশ্য নয়।
কারণ এখানে গণিত নিয়েই লিখব বলে স্থির করেছি। তবে এপোস্তলস দক্সিয়াদিস এই উপন্যাসের প্লট
কোথা থেকে পেয়েছেন এ ব্যাপারে আমার একটা অনুমান আছে যদিও দক্সিয়াদিস কোথাও তা লিখেন নি। আমার
বিশ্বাস একটি বাস্তব
জীবন থেকেই তিনি এই উপন্যসের প্লটটি নিয়েছেন। এ প্রসঙ্গে পরে আসব। আপাতত মৌলিক সংখ্যা
নিয়ে কিছু আলোচনা করা যাক। কারণ গোল্ডবাক কনজেকচারের সমস্যাটি জড়িয়ে আছে মৌলিক সংখ্যার
বিন্যাসে উপর যার আজ অব্ধি কোন অর্ডার বা শৃঙ্খলা পাওয়া যায় নি। এই পর্ব শেষ করার
আগে একটা মজার কথা বলে নিই। গোল্ডবাক তার ডায়েরিতে লিখে দেন যে তিনি এই সমস্যার সমাধান করে
ফেলেছেন তবে ডায়েরিতে
জায়গার অভাবে ওখানে তিনি তা লিখতে পারছেন না। তিনি মারা যাবার পর তাঁর বাড়িতে তন্ন
তন্ন করে খুঁজেও এরকম কোন খাতা কিংবা অন্য কোন ডায়েরি পাওয়া যায় নি যেখানে তিনি এর সমাধান
লিখে রেখে গেছেন। বর্তমানে গণিতজ্ঞরা বিশ্বাস করেন যে তিনি মিথ্যে কথাই লিখেছিলেন। এই নিয়ে পরে অনেক
মজাদার ঘটনা ঘটেছে
যা পরে লিখব। এখানে উপন্যাসের প্রচ্ছদ ও গোল্ডবাকের ছবি দেওয়া হলো।
রিমেন হাইপথেসিস ও মৌলিক সংখ্যার
শৃঙ্খলা আবিষ্কারে সমস্যা
পদার্থের মধ্যে যেমন মৌলিক ও যৌগিক পদার্থ আছে
তেমনি সংখ্যার ক্ষেত্রেও তা আছে। যেমন হাইড্রোজেন ও অক্সিজেন হলো দুটো মৌলিক পদার্থ এবং এই
দুয়ের রাসায়নিক যৌগ
হল হল জল। যারা ধর্মীয় কথা শুনতে ভালবাসেন তাদের বলি যে রাম ও কৃষ্ণ হলেন দুজন মৌলিক
অবতার এবং রামকৃষ্ণ হলেন এই দুজনের যৌগিক অবতার। মৌলিক সংখ্যা হলো একের চাইতে বড় সেই সংখ্যা
যার ১ ও ওই সংখ্যা ছাড়া আর কোন উৎপাদক নেই। যেমন ২, ৩,
৫, ৭, ১১,
১৩, ১৭ ইত্যাদি। এই সারিতে ৪, ৬, ৮,
৯, ১০, ১২,
১৪, ১৫, ১৬
সংখ্যাগুলো আসেনি কারণ কোন দুই বা ততোধিক সংখ্যার গুণফল দিয়ে
এই সংখ্যাগুলোকে প্রকাশ করা যায়। এই
মৌলিক সংখ্যা হলো একেবারে মূল সংখ্যা যেগুলো স্বয়ংসম্পূর্ণ। অন্য সংখ্যার গুণিতক নয়। তাই আমার
বিশ্বাস মৌলিক সংখ্যাগুলোকে
শাস্ত্রকাররা পবিত্র হিসেবে গণ্য করতেন। যেমন পঞ্চগব্য, সাতপাক, ত্রিফলা,
পঞ্চভূত, সপ্তঋষি ইত্যাদি। তবে এটা আমার অনুমান। কারণ গণিতজ্ঞদের মধ্যেও
মৌলিক সংখ্যা নিয়ে দুর্বলতা আছে। যেমন ইংল্যান্ডের এক বিশিষ্ট গণিতজ্ঞ তাঁর ডায়েরিতে দশটি
ইচ্ছার কথা লিখে যান। এর মধ্যে ‘হিটলারকে
হত্যা’ যেমন আছে তেমনি ওভেল
স্টেডিয়ামে ২১১ রান করার কথাও আছে। প্রশ্ন হলো ২০০ না লিখে ২১১ কেন? কারণ ২০০ একটি মৌলিক সংখ্যা নয় এবং ২০০-র
পর ২১১-ই প্রথম মৌলিক সংখ্যা।
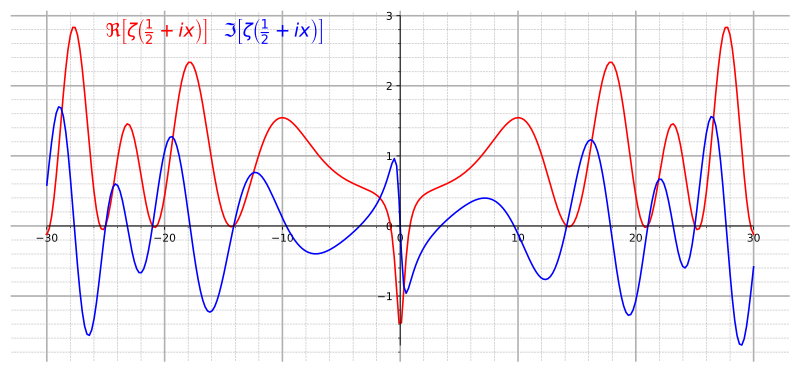
মৌলিক সংখ্যা নিয়ে সবচাইতে জনপ্রিয় সমস্যাটি হলো
রিমেন হাইপথেসিস (Riemann hypothesis) । হাইপথেসিস শব্দের অর্থ হলো যা সত্য হিসেবে প্রমাণিত হয় নি অথচ সত্য বলে
মনে হয় এবং অসত্য
হিসেবেও প্রমাণ করা যায় নি। যেমন রিমেন হাইপথেসিসকে কেউ প্রমাণ করতে পারে নি এটা সত্যি নয়
এবং গাণিতিক যুক্তি দিয়ে প্রমাণ করা যায় নি যে এই অনুমান সত্যি। তাই এখনও এটা একটা
হাইপথেসিস। যদি কোন দিন এটা প্রমাণ হয়ে যায় যে এই অনুমান সত্যি নয় তাহলে তা
খারিজ হয়ে যাবে। আবার যদি গাণিতিক যুক্তি দিয়ে প্রমাণিত হয় যে এটা সত্যি তাহলে এটা আর হাইপথেসিস
থাকবে না, হয়ে যাবে গাণিতিক
সিদ্ধান্ত। কনজেকচারের অর্থও মোটামুটি একই। তবে রিমেন হাইপথেসিস গোল্ডবাখ কনজেকচারের মতো এত
সরল নয় যে স্কুলের একটি মাঝারি ছাত্রও তা বুঝতে পারে। এটি কিছুটা উন্নতমানের যেখানে অসীম
সংখ্যা পর্যন্ত মৌলিক
সংখ্যার জিটা ফাংশন নিয়ে এমন এক অনুমানের কথা বলা হয়েছে যা ১৮৫৯ সাল থেকে বহু চেষ্টার পরও
প্রমাণ করা যায় নি। আবার এর সত্যতাকে খারিজও করে দেওয়া যায় নি।
রিমেন হাইপথেসিসকে গণিতজ্ঞরা এতটাই সত্য হিসেবে ধরে নিয়েছেন
যে কয়েক’শ গবেষকরা ইতিমধ্যেই
ডক্টরেট ডিগ্রি পেয়ে গেছেন যেখানে তাদের গবেষণা পত্রের কোন কোন জায়গায় লেখা আছে ‘যদি রিমেন হাইপথেসিস সত্যি হয় তাহলে ...’। যদি কোনদিন এই রিমেন হাইপথেসিস মিথ্যে
হিসেবে প্রমাণিত
হয়ে যায় তাহলে এই ডক্টরেট ডিগ্রিগুলোর কি হবে তা ঈশ্বরই জানেন। গণিতজ্ঞদের দৃঢ়
বিশ্বাস যে রিমেন হাইপথেসিস ভুল হিসেবে প্রমাণিত হবে না। তবে রিমেন হাইপথেসিস কিংবা গোল্ডবাখ
কনজেকচার থেকে একটা জিনিস বুঝা যায় যে মৌলিক সংখ্যার একটা শৃঙ্খলা আছে। কিন্তু এই শৃঙ্খলা আবিষ্কার
করাটাই হয়ে গেছে
গণিতজ্ঞদের কাছে সবচেয়ে বড় চ্যালেঞ্জ। রিমেন হাইপথেসিসকে প্রমাণ করতে পারলে এই শৃঙ্খলা
আবিষ্কার হয়ে যাবে। যিনি এটা আবিষ্কার করবেন তিনি গণিতের জগতে পেয়ে ঈশ্বরতূল্য সম্মান। এর জন্য অনেক অনেক পুরস্কারের
কথা ঘোষণা করা আছে।
তবে তার আগে রিমেন হাইপথেসিস নিয়ে একটি মজার ঘটনার কথা বলে নিই যা থেকে বুঝা যাবে এই
সমস্যার সমাধান গণিতজ্ঞদের কাছে কত বড় স্বপ্ন।
যে গণিতজ্ঞ দশটি স্বপ্নের কথা লিখেছিলেন
তিনি তাঁর ডায়েরিতে রিমেন হাইপথেসিস সমাধানের কথাও লিখেছেন। তবে কাণ্ড করেছিলেন জি এইচ হার্ডি যিনি
রামানুজনকে নিয়ে
গিয়েছিলেন ইংল্যান্ডে। হার্ডি যখন জাহাজে করে স্ক্যান্ডিনেভিয়া থেকে ইংল্যান্ড আসছিলেন
তখন হঠাৎই সমুদ্রে ঝড় ওঠায় বাউল বাতাসে জাহাজটি টলমল হতে থাকে। জাহাজ ডুবে যেতে পারে এই আশঙ্কায়
যাত্রীদের মধ্যে তখন ত্রাহি ত্রাহি রব। এই সময়ে হার্ডি একটি পোস্টকার্ডে তাঁর বন্ধুর নামে একটি
চিঠিতে লিখে ফেলেন
যে তিনি রিমেন হাইপথেসিসের সমাধান করে ফেলেছেন। তবে জাহাজে পর্যাপ্ত কাগজ না থাকায় তিনি
তা লিখতে পারছেন না তাই দেশে ফিরে গিয়ে তা লিখবেন। এই কার্ডটিকে তিনি এমনভাবে রেখে দেন যাতে
জাহাজ ডুবে গেলেও কার্ডটি জলে ভিজে নষ্ট হবে না। শেষ পর্যন্ত ঝড় থামে এবং যাত্রীরা নিরাপদে দেশে
ফেরেন।
ইংল্যান্ডে ফিরে আসার পর হার্ডি জানান যে তিনি
ঈশ্বরের সঙ্গে চালবাজি করে ঝড়টি থামিয়েছেন। কারণ একদিন না একদিন এই ডুবন্ত জাহাজ থেকে তাঁর
লেখা কার্ডটি উদ্ধার
হবে। তখন অনেকেই ভাববেন হার্ডি সত্যি সত্যিই রিমেন হাইপথেসিসের সমাধান করে ফেলেছিলেন
কিন্তু লিখে যেতে পারেন নি। হার্ডি তো সাধারণত মিথ্যে কথা বলেন না তাই লোকের পক্ষে এটা
বিশ্বাস করাটা কঠিন হবে না। অর্থাৎ কিছু না করেই তিনি এমন এক সম্মানের অধিকারী
হয়ে যাবেন যা অতি বিরল। ঈশ্বর কখনই চাইবেন না যে কিছু না করে কেউ এতটা খ্যাতি অর্জন করে নিক। তাই
ঈশ্বরের কাছে ঝড়
থামিয়ে হার্ডিকে নিরাপদে দেশে ফিরিয়ে এনে তাঁর মিথ্যাচারকে ধরিয়ে দেওয়া ছাড়া আর কোন উপায় ছিল
না, তাই বাধ্য হয়ে তিনি সামুদ্রিক ঝড়কে
থামিয়েছেন। অর্থাৎ
হার্ডি ঈশ্বরকে বেকায়দায় ফেলে তাঁকে দিয়ে ঝড়কে থামিয়ে দিয়েছেন। হার্ডির যদিও মজা করে
তা বলেছিলেন তবে এই গল্প শোনার পর গণিতের এক ছাত্র নিউইয়র্ক শহরের সেন্ট্রাল মেট্রো রেলের
দেওয়ালে লিখে দিয়েছিল সে রিমেন হাইপথেসিসের সমাধান করে ফেলেছে কিন্তু তার ট্রেন এসে পড়ায় সে
তা লিখে রাখার সময়
পাচ্ছে না।
রিমেন হাইপথেসিসকে প্রমাণ করা প্রতিজন গণিতজ্ঞের স্বপ্ন।
কারণ যিনি এটা প্রমাণ করবেন তিনি পাবেন বিপুল পরিমাণ অর্থ ও গণিতের জগতে অপরিসীম প্রতিপত্তি।
আমেরিকার ক্লে ম্যাথেমেটিক্স ইন্সটিটিউট সাতটি সমস্যার উল্লেখ করে জানিয়েছে এর প্রতিটির
সমাধানের জন্য দেওয়া
হবে দশ লক্ষ করে মার্কিন ডলার। এই সাতটির মধ্যে রিমেন হাইপথেসিসকে রাখা হয়েছে
সর্বোচ্চে। তবে প্রশ্ন হলো গোল্ডবাখ কনজেকচারকে কেন রাখা হয় নি। এর কারণ আমি চিন্তা
করে দেখেছি যে রিমেন হাইপথেসিসের সমাধান হয়ে গেলে মৌলিক সংখ্যার শৃঙ্খলা বেরিয়ে পড়বে। এই
শৃঙ্খলা বেরিয়ে গেলে গোল্ডবাখ কনজেকচারের সমাধান এমনিতেই হয়ে যাবে। তাই দুটোকে রাখার প্রয়োজন
নেই।
মৌলিক সংখ্যার শৃঙ্খলা বা ফরমুলা বের করাটা
বর্তমানে ভীষণ জরুরি হয়ে পড়েছে। বিশেষ করে সারা বিশ্বজুড়ে ইন্টারনেট ব্যাংকিং ব্যবস্থায় যে
ভাবে পাসওয়ার্ডকে
সংরক্ষিত রাখা হয় তা অনেক সময়েই হ্যাকিং হয়ে যায়। এর জন্য বহু মিলিয়ন ডলারের লোকসান
হয়ে যায় ব্যাংক ও অন্যান্য আর্থিক সংস্থাগুলোর। এই নিয়ে কম্পিউটার সফটওয়্যার বিশেষজ্ঞরা
বহুদিন ধরেই চিন্তিত। এই হ্যাকিং বন্ধ করার কোন উপায় তারা খুঁজে পাচ্ছেন না। তবে তারা একটি উপায়
আবিষ্কার করেছেন কিন্তু
এর জন্য মৌলিক সংখ্যার শৃঙ্খলা জানা দরকার। তাই রিমেন হাইপথেসিসকে সমাধান করার জন্য
কয়েকটি মার্কিন কোম্পানি উঠে পড়ে লেগেছে। এই কোম্পানিগুলো প্রতিভাবান গণিতজ্ঞদের বিশাল অংকের বেতন
দিয়ে রেখেছে আর এই গণিতজ্ঞরা যাতে বেতন নিয়ে অসফল হওয়ার বেদনায় না ভোগেন তাই কোম্পানি থেকে তাদের
বলে দেওয়া হয়েছে
যে তারা যে সমাধান করতে পারবেন কোম্পানি তা আশা করে না। শুধু
প্রচেষ্টা চালানোর জন্যই তাদের রাখা
হয়েছে।
গণিতজ্ঞরা মনে করেন আগামী এক শতকের মধ্যে এটা আবিষ্কার
হওয়ার কোন আশা তারা দেখতে পাচ্ছেন না। মৌলিক সংখ্যার শৃঙ্খলা আবিষ্কার করার চেষ্টা বহু শতাব্দী
ধরেই চলছে কিন্তু
সমস্ত প্রচেষ্টা এ যাবত ব্যর্থ হয়েছে। কেউ কেউ বলছেন এই আবিষ্কার সম্ভব নয় কারণ একজন
বিশাল প্রতিভাসম্পন্ন গণিতজ্ঞকে তার জীবনের উজ্জ্বল ভবিষ্যৎ, সুখী পরিবারসহ সব কিছু ছেড়ে দিয়ে শুধুমাত্র এই কাজে আত্মনিয়োগ করতে হবে যেখানে
সাফল্যের চান্স প্রায় শূন্য। এরকম গণিতজ্ঞ কয়জন আছেন। অর্থাৎ কয়েক’শ আঙ্কল পেত্রোস জন্মানোর পরই এর সমাধান সম্ভব।
রিমেন হাইপথেসিস যার নামের সঙ্গে যুক্ত তিনি
হলেন গিয়র্গ ফ্রেডরিখ বার্নহার্ড রিমেন যিনি জাতিতে জার্মান এবং তিনি ১৮২৬ সালের ১৭ সেপ্টেম্বর
তারিখে জন্মেছিলেন
জানোভার রাজ্যের ব্রেসেলেঞ্জ গ্রামে। এই গ্রামটি বর্তমানে ফেডারেল রিপাবলিক অব জার্মানির
অন্তর্ভুক্ত। জার্মানির গোটিনজেন ও বার্লিন বিশ্ববিদ্যালয়ের কৃতি ছাত্র হিসেবে তাঁর
সুখ্যাতি তো ছিলই। এছাড়া সংখ্যাতত্ত্ব ও ডিফারেন্সিয়াল জিওমেট্রিতেও তাঁর প্রচুর অবদান
রয়েছে। এমন কি
আইনস্টাইনের জেনারেল থিওরি অব রিলেটিভিটি আবিষ্কারের পেছনেও রিমেনের অবদান অনস্বীকার্য।

কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন